Spring Mass Damper System Differential Equation
Spring mass damper system differential equation. The general solution will be uleft t right u_cleft t right U_Pleft t right. When the viscous properties of the fluid in the buffer remain constant an ordinary differential equation of the second order serves as a mathematical model. Forward Euler approximation of the undamped mass-spring system h 001 The backward Euler method is defined as yn1 yn y n1h.
A-First order B-Second order C-Third order 2How can a dynamic system be put into motion. Dydt x 2. From the above equation it is clear that the period of oscillation is free from both gravitational acceleration and amplitude.
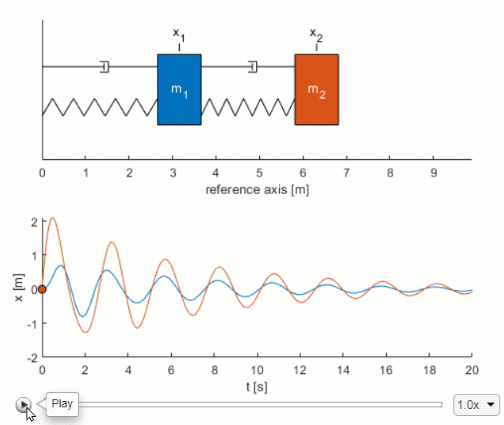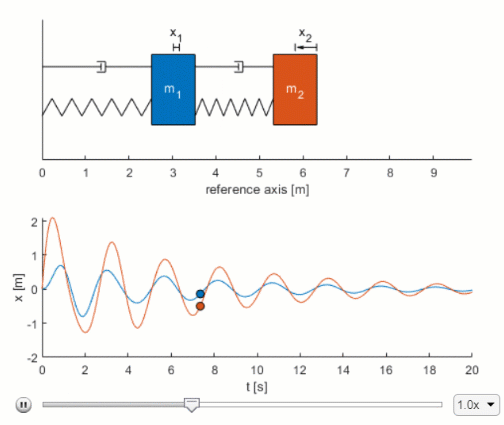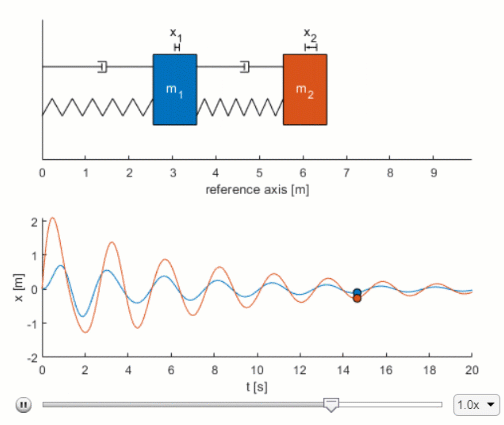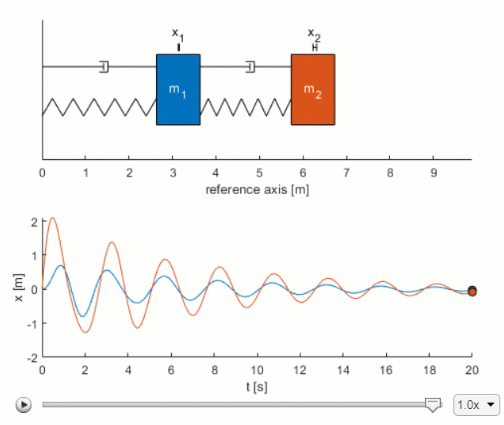
Presents a canonical mass-spring-damper system and derives the governing differential equation. Energy in a spring-mass system A horizontal spring-mass system has low friction spring stiffness 170 Nm and mass 0. The complementary function which arises solely due to the system itself and the particular integral which arises solely due to the applied forcing term.
S2 4s 4 0. Divide the equation through by m. N 0 and call n the natural circular frequency of the system.
Because the roots are repeated the system is critically damped. So x t e 2t 1 2t. That is to say the evolution of said mechanical oscillations can be predicted when studying the analytical solution of said equation.
So we have a mass spring system which is supposed to be modelling a bridge and the equation that the displacement of the bridge x satisfies is given by. Ylabel Position Speed m ms xlabel Time s title mass-spring-damper system. 0 1 2 3 4 5 00 02 04 06 08.
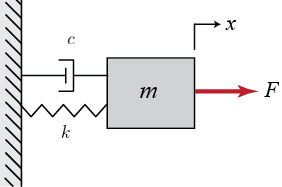
This factors 2 2. BACKGROUND MATH The time domain equation of motion for the mass-spring-damper is represented by Newtons Second Law written as the fol-lowing force balance on a structure 𝐌 𝐱 𝐂 𝐱 𝐊 𝐱 M Mass C Damping K Stiffness.
Xbmx n2x 0.
Function dydt odefun x F 1x 13 - 1x 12 1x 1. K 361 107. What is the general solution to the differential equation describing a mass-spring-damper. F t l y dt dy R dt d y M λ 2 2. BACKGROUND MATH The time domain equation of motion for the mass-spring-damper is represented by Newtons Second Law written as the fol-lowing force balance on a structure 𝐌 𝐱 𝐂 𝐱 𝐊 𝐱 M Mass C Damping K Stiffness. Presents a canonical mass-spring-damper system and derives the governing differential equation. From the above equation it is clear that the period of oscillation is free from both gravitational acceleration and amplitude. One can buy dampers the shock absorbers in your car contain dampers. A spring-mass-damper-system is an approximation of a dynamic system having an energy conserving spring part an energy dissipating damper and an inertial mass part.
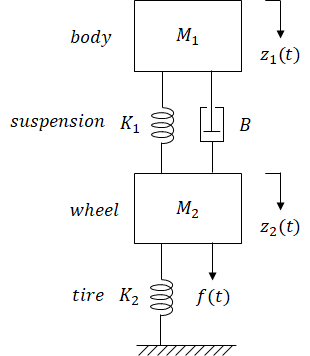
K 361 107. Similar to FEM the whole body is discretised into springs and dampers in series or parallel with. The damping coefficient c is simply defined as the damping force divided by shaft velocity. Because the roots are repeated the system is critically damped. Based on Newtons second law. Divide the equation through by m. Ylabel Position Speed m ms xlabel Time s title mass-spring-damper system.



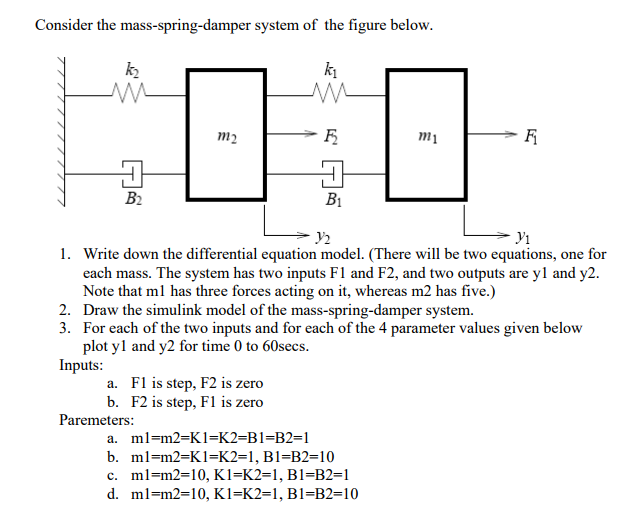

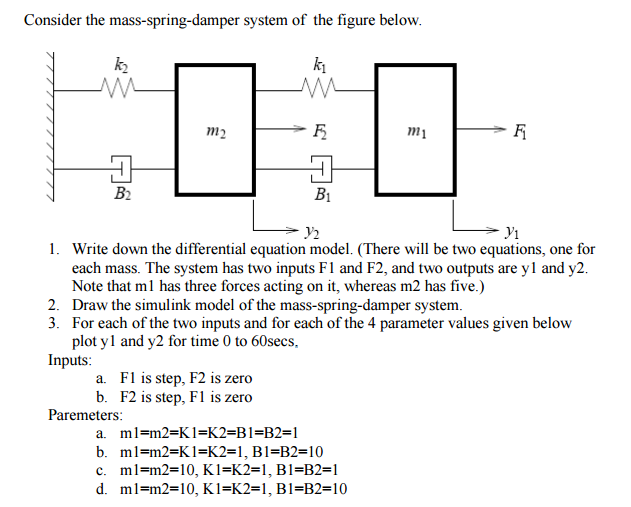










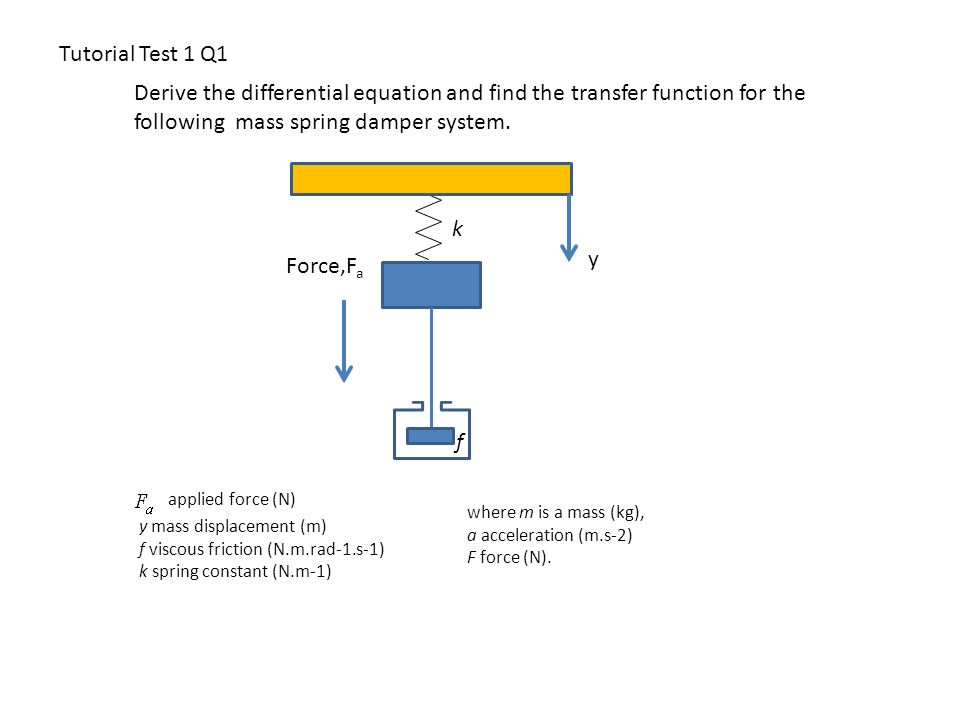
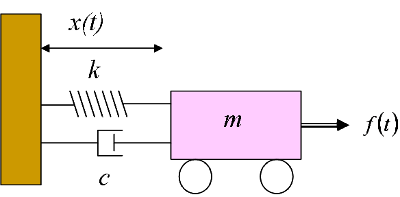









Post a Comment for "Spring Mass Damper System Differential Equation"