Turn Second Order Ode Into System
Turn second order ode into system. A typical approach to solving higher-order ordinary differential equations is to convert them to systems of first-order differential equations and then solve those systems. A second-order ODE is called linear if it can be written 1 y pxy qxy rx and nonlinear if it cannot be written in this form. Every ODE can be converted into first order and generically into one of the form u F u where u is a vector valued function on some interval of real numbers.
But since it is not a prerequisite for this course we have to limit ourselves to the simplest. 23 Second order ODE flow The ODE systems are denoted as continuous normalizing flows when they are applied on random variables z tRezende et al2014Chen et al2018aGrathwohl et al2018. Left m2 11m 24 right 0 Factor it.
Systems of First Order Linear Differential Equations We will now turn our attention to solving systems of simultaneous homogeneous first order linear differential equations. Solution plot for the initial value problem y00 5y0 6y 0 y0 0 y00 1 using Simulink. Or equivalently x 3 4 x 3 x 2 2 x 1.
Replacing we have the x 3 4 x 3 x 2 2 x 1 0. If you have a single second-order ODE an ODE containing a second-derivative you can actually just use a simpler substitution trick to transform it into a system of two first-order ODEs which you can solve using by finding the eigenvalues and eigenvectors. You dont have to show all the algebra steps to summarize these substitutions will turn the second-order ODE into what looks like a quadratic equation which we can factor and find the solution to.
Harris in Mathematics for Physical Science and Engineering 2014 Solutions and Boundary Conditions. Second order differential equations 45 x 0 05 1 15 2 25 3 35 4 45 5 y 0 005 01 015 yx vs x Figure 34. The solutions of such systems require much linear algebra Math 220.
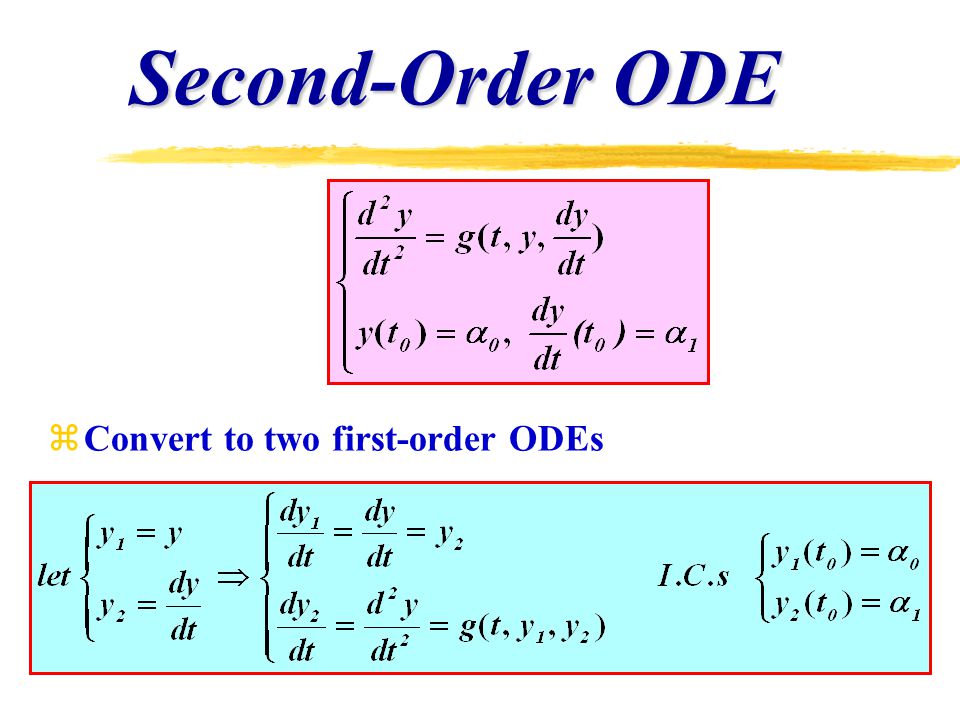
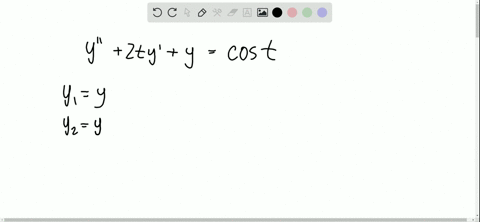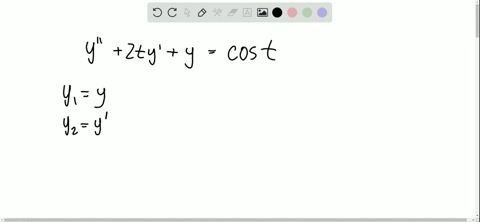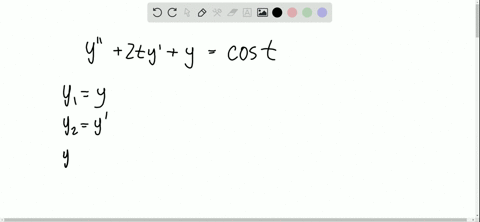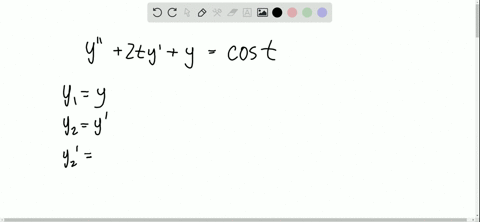
Read rx is identically zero then 1 reduces to 2 y pxy qxy 0 and is called homogeneous. Ytsinyt0 y01 y00 Homework Equations The Runge-kutta method might be applicable but I know how to do that part no problem. To convert second-order ODE to a first-order system you have to introduce new variables.
Beginalign fracdxdt u fracdudt frac1mFt- eta u - kx. We can write higher order differential equations as a.
Ytsinyt0 y01 y00 Homework Equations The Runge-kutta method might be applicable but I know how to do that part no problem.
2y 5y y 0 y3 6 y3 1 2 y 5 y y 0 y 3 6 y 3 1. If rx 0 that is rx 0 for all x considered. We can write higher order differential equations as a. As far as I experienced in real field in which we use various kind of engineering softwares in stead of pen and pencil in order to handle various real life problem modeled by differential equations. Beginalign fracdxdt u fracdudt frac1mFt- eta u - kx. Replacing we have the x 3 4 x 3 x 2 2 x 1 0. Then it uses the MATLAB solver ode45 to solve the system. Convert the following second-order differential equation into a system of first-order equations and solve y1 and y1 with 4th-order Runge-kutta for h05. In general given a second order linear equation with the y-term missing y pt y gt we can solve it by the substitutions u y and u y to change the equation to a first order linear equation.
If F is sufficiently smooth Lipschitz continuous then for any choice of initial value u 0 there is a unique solution. Recall the solution of this problem is found by first seeking the. We can write higher order differential equations as a. A typical approach to solving higher-order ordinary differential equations is to convert them to systems of first-order differential equations and then solve those systems. The solutions of such systems require much linear algebra Math 220. Gx y fracdydx fracd2ydx2 0 and the general explicit form is. Example 1 Write the following 2 nd order differential equation as a system of first order linear differential equations.


































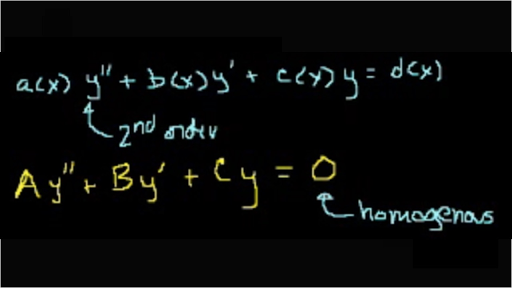





Post a Comment for "Turn Second Order Ode Into System"